Coefficient of Determination

  • Correlation Coefficient Squared
  • Percentage of the variability among scores on one variable that can be attributed to variability in the scores on the other variable

One way researchers often express the strength of the relationship between two variables is by squaring their correlation coefficient. Suppose a group of students was administered a reading achievement test and a verbal IQ test. If the students’ reading achievement scores and verbal IQ-test scores had a correlation of 0.80, a researcher might report the squared correlation as 0.80 times 0.80 = 0.64. This squared correlation coefficient is called a COEFFICIENT OF DETERMINATION.

The coefficient of determination is useful because it gives the proportion of the variance (fluctuation) of one variable that is associated with fluctuation in the other variable. 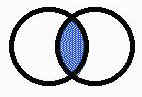graphic of r square

So we might say that 0.64 (or 64%) of the variance of the students’ reading achievement scores is predictable from their verbal IQ-test scores. If two variables had a correlation of plus or minus 1.00, the corresponding coefficient of determination would equal +1.00. This would mean that 100% of the variance of one variable would be predictable using the other variable, and vice versa…Conversely, suppose that two variables had a correlation of zero. Then the coefficient of determination would equal zero, suggesting that none of the variance of one variable was linearly predictable from the other variable. (Jaeger, 1990, p.67)

Jaeger, R. M. (1990). Statistics: A spectator sport (2nd ed.). Newbury Park, CA: Sage Publication.

Note: The author writes “predictable” not “caused”

Del Siegle, Ph.D.
Neag School of Education – University of Connecticut
del.siegle@uconn.edu
www.delsiegle.com